This project is a PyTorch-inspired deep learning framework built from scratch, not aimed at competing with established frameworks but to provide a deeper understanding of how deep neural networks work under the hood. The goal is to recreate the core functionality of PyTorch, including tensor operations, automatic differentiation, and basic deep learning layers, while keeping the implementation simple and transparent for learning purposes.



Motivation
The main goal of this project is to understand how deep learning frameworks work by building one from scratch. This clone breaks down the complexities into simpler parts, making it easier to understand and providing insights into:
- How tensors are represented and manipulated.
- How gradients are computed through the computational graph.
- How various layers and optimizers are implemented.
- How forward and backward passes work in a neural network.
What was actually implemented
- Tensors:
- class that wraps numpy (or cupy for cuda usage) for values and gradients.
- Allow view to get slice of tensor.
- Layers:
- Linear (Dense)
- Conv2D
- Operations:
- Basic : +, *, -, / with backward propagation
- Activation : tanh, relu, softmax with backward propagation
- Other functions : abs, pow, log, exp with backward propagation
- Basic losses : mse, mae, categorical cross entropy
- Optimizer:
- SGD (mini batch gradient)
- RMSProp
- Adam
- AdamW
- NAdam
Code sample
from src.pynn.layers.conv_2d import Conv2d
from src.pynn.layers.dense import Dense
from src.pynn.tensor import Tensor
from src.pynn.graph import ComputeGraph
from src.pynn.optimizers import SGD, Adam, Optimizer
from src.pynn.math import *
from src.pynn.losses import categorical_cross_entory
from src.pynn.models.model import Model
from src.pynn import Flags
import numpy as np
from tqdm import trange
batch_size = 64
num_epoch = 10
num_batch = 900
x_input = Tensor.randn((batch_size, 784))
x = Dense(784, 256, relu)(x_input)
x = Dense(256, 128, relu)(x)
x = Dense(128, 32, relu)(x)
x = Dense(32, 10, softmax)(x)
model = Model(x_input, x)
opt = Adam(0.01)
final_train_image = np.array(train_images, dtype=Flags.global_type()) / 255.
Xdata = Tensor.from_values(final_train_image)
Ydata = Tensor.from_values(train_labels_one_hot)
for epoch in range(1, num_epoch + 1):
bar = trange(1, num_batch + 1)
bar.set_description(f"Epoch {epoch}")
eloss = 0
eaccuracy = 0
for current_batch in bar:
Xbatch = Xdata[current_batch * batch_size:(current_batch + 1) * batch_size]
Ybatch = Ydata[current_batch * batch_size:(current_batch + 1) * batch_size]
pred = model(Xbatch)
loss = categorical_cross_entory(pred, Ybatch)
loss.zero_grad()
loss.backward()
opt.update(model.parameters)
eloss += loss.values
eaccuracy += batch_accuracy(pred, Ybatch) # batch accuracy is a custom function that calculate ratio
# true_pred / total_pred
bar.set_postfix({"Loss" : eloss[0] / current_batch})
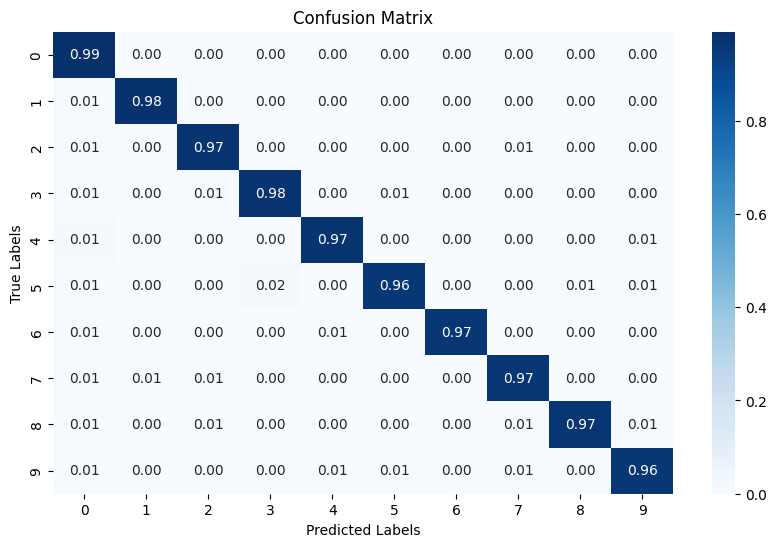
output:
| Epoch 1: 100% | ██████████ | 900/900 [00:17<00:00, 50.07it/s, Loss=0.267, accuracy=0.921] |
| Epoch 2: 100% | ██████████ | 900/900 [00:15<00:00, 58.18it/s, Loss=0.108, accuracy=0.968] |
| Epoch 3: 100% | ██████████ | 900/900 [00:15<00:00, 57.19it/s, Loss=0.0757, accuracy=0.977] |
| Epoch 4: 100% | ██████████ | 900/900 [00:14<00:00, 62.47it/s, Loss=0.061, accuracy=0.982] |
| Epoch 5: 100% | ██████████ | 900/900 [00:15<00:00, 58.31it/s, Loss=0.0511, accuracy=0.984] |
| Epoch 6: 100% | ██████████ | 900/900 [00:15<00:00, 56.86it/s, Loss=0.0404, accuracy=0.988] |
| Epoch 7: 100% | ██████████ | 900/900 [00:19<00:00, 46.48it/s, Loss=0.0382, accuracy=0.988] |
| Epoch 8: 100% | ██████████ | 900/900 [00:17<00:00, 50.48it/s, Loss=0.034, accuracy=0.989] |
| Epoch 9: 100% | ██████████ | 900/900 [00:19<00:00, 46.03it/s, Loss=0.0324, accuracy=0.99] |
| Epoch 10: 100% | ██████████ | 900/900 [00:16<00:00, 55.61it/s, Loss=0.0309, accuracy=0.991] |

Important Considerations
The convolution operation works as expected, producing correct outputs and gradients. However, the calculations are not fully vectorized yet, which means that convolutional layers might not perform as fast as expected. This is in contrast to other operations in the framework (such as tensor addition, multiplication, and activation functions), which are fully vectorized and run efficiently.
Optimizing the convolution operation is on my todo-list, and future updates will focus on ensuring that it achieves similar performance to other operations. For now, convolution is still functional but not as optimized as possible.
